A)
B)
C) 2
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write the complex number in polar form. Express the argument in degrees, rounded to the nearest tenth, if necessary. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Choose the one alternative that best completes the statement or answers the question. The polar coordinates of a point are given. Find the rectangular coordinates of the point. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the distance from P1 to P2. - and
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the angle between v and w. Round your answer to one decimal place, if necessary. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area of the parallelogram. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. Round your answer to the nearest tenth. -A person is pulling a freight cart with a force of 40 pounds. How much work is done in moving the cart 30 feet if the cart's handle makes an angle of 22° with the ground?
A) 1,112.6 ft-lb
B) 45.0 ft-lb
C) 449.5 ft-lb
D) 1,147.6 ft-lb
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the polar equation.
-
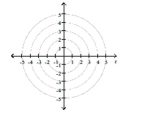
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The rectangular coordinates of a point are given. Find polar coordinates for the point. - Round the polar coordinates to two decimal places, with in degrees.
A)
B)
C)
D)
Correct Answer

verified
C
Correct Answer
verified
Multiple Choice
Choose the one alternative that best completes the statement or answers the question. Find the direction angles of the vector. Round to the nearest degree, if necessary. -
A)
B)
C)
D)
Correct Answer

verified
A
Correct Answer
verified
Multiple Choice
Plot the point given in polar coordinates.
-
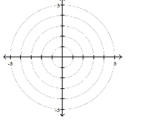
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the unit vector having the same direction as v. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Essay
Write the word or phrase that best completes each statement or answers the question. Solve the problem. -Find a unit vector normal to the plane containing
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. Leave your answer in polar form. - Find .
A)
B)
C)
D)
Correct Answer

verified
C
Correct Answer
verified
Multiple Choice
Write the complex number in rectangular form. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
-
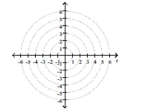
A) ![]()
B) ![]()
; vertical line 4 units
to the left of the pole
C) ![]()
; vertical line 4 units
to the right of the pole
D) ![]()
; horizontal line 4 units
below the pole
; horizontal line 4 units
above the pole
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the indicated cross product. - Find .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Test the equation for symmetry with respect to the given axis, line, or pole. -
A) Symmetric with respect to the pole
B) May or may not be symmetric with respect to the pole
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Match the point in polar coordinates with either A, B, C, or D on the graph.
-
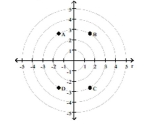
A) A
B) B
C) C
D) D
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Choose the one alternative that best completes the statement or answers the question. The polar coordinates of a point are given. Find the rectangular coordinates of the point. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Showing 1 - 20 of 253
Related Exams