A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the coordinates of the other endpoint of the segment, given its midpoint and one endpoint. -midpoint , endpoint
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the three points are collinear. -Which graphs of functions increase over the whole of their domain?
A) graphs A and B
B) graphs C and D
C) graphs A and D
D) graph D
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such.
-
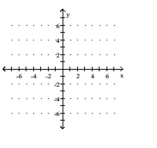
A) , ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the slope of the line and sketch the graph.
-
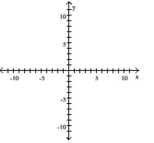
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the center and radius of the circle. -
A) center: ; radius: 81
B) center: ; radius: 9
C) center: ; radius: 81
D) center: ; radius: 9
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A new chocolate company is estimating how many candy bars per week college students will consume of their line of
products. The graph shows the probable number of candy bars students (age 18-22) will consume from year 0 to year 10.
B(x) gives the number of candy bars for boys, G(x) gives the number of candy bars for girls, and T(x) gives the total
number for both groups. Use the graph to answer the question. 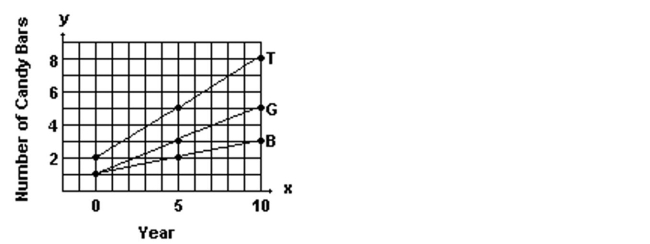 -The radius of a circle of known area is given by , where . Find the radius and circumference of a circle with an area of . (Round results to two decimal places.)
-The radius of a circle of known area is given by , where . Find the radius and circumference of a circle with an area of . (Round results to two decimal places.)
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the line and give the domain and the range.
-
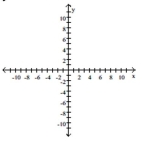
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the intervals of the domain over which the function is continuous.
-P(2, 3) ![Determine the intervals of the domain over which the function is continuous. -P(2, 3) A) ( - \infty , 2 ] \cup [ 2 , \infty ) B) ( - \infty , 3 ) \cup ( 3 , \infty ) C) ( - \infty , 2 ) \cup ( 2 , \infty ) D) ( - \infty , \infty )](https://d2lvgg3v3hfg70.cloudfront.net/TB7516/11ecc541_8a65_b494_8347_493bbccbaf7d_TB7516_11.jpg)
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Describe how the graph of the equation relates to the graph of y .
-
![Describe how the graph of the equation relates to the graph of y y = \sqrt [ 3 ] { x } . - f(x) =-(x-6) ^{2}-2 A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB7516/11ecc546_ff9c_04ad_8347_d3f06d11ccef_TB7516_11.jpg)
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Compute and simplify the difference quotient -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Describe how the graph of the equation relates to the graph of y .
-
![Describe how the graph of the equation relates to the graph of y y = \sqrt [ 3 ] { x } . - f ( x ) = \frac { 1 } { 3 } | - x | A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB7516/11ecc545_5812_1d27_8347_819fb3ca27f6_TB7516_11.jpg)
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Decide whether the relation defines a function. -
A) Function
B) Not a function
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the point symmetric to the given point.
-
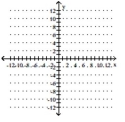
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the equation by plotting points.
-
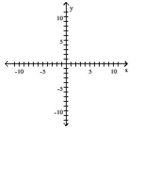
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write an equation for the line described. Give your answer in slope-intercept form. - , through
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Give a rule for the piecewise-defined function. Then give the domain and range.
-![Give a rule for the piecewise-defined function. Then give the domain and range. - A) f ( x ) = \left\{ \begin{array} { l l } x ^ { 3 } & \text { if } x < 1 \\ x + 4 & \text { if } x \geq 1 \end{array} ; \right. Domain: ( \infty , \infty ) , Range: ( \infty , 1 ) \cup [ 5 , \infty ) B) f ( x ) = \left\{ \begin{array} { l l } x ^ { 3 } & \text { if } x < 1 \\ x - 4 & \text { if } x \geq 1 \end{array} ; \right. Domain: ( \infty , 1 ) \cup [ 5 , \infty ) , Range: ( \infty , \infty ) C) f ( x ) = \left\{ \begin{array} { l l } \sqrt [ 3 ] { x } & \text { if } x < 1 ; \text { Domain: } ( \infty , \infty ) , \text { Range: } ( \infty , 1 ) \cup [ 5 , \infty ) \\ x + 4 & \text { if } x \geq 1 \end{array} \right. D) f ( x ) = \left\{ \begin{array} { l l } - x ^ { 3 } & \text { if } x < 1 \\ x - 4 & \text { if } x \geq 1 \end{array} ; \right. Domain: ( \infty , 1 ) \cup [ 5 , \infty ) , Range: ( \infty , \infty )](https://d2lvgg3v3hfg70.cloudfront.net/TB7516/11ecc542_b08d_5b1e_8347_3b0ff7396278_TB7516_11.jpg)
A) Domain: , Range:
B) Domain: , Range:
C)
D) Domain: , Range:
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such.
-
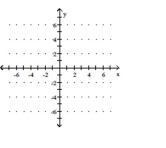
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
For the pair of functions, find the indicated sum, difference, product, or quotient. - Find .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the specified domain. -Find the domain of when and
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Showing 261 - 280 of 531
Related Exams