A) at
B) at
C) at
D) at
Correct Answer

verified
Correct Answer
verified
Multiple Choice
For the pair of functions, find the indicated sum, difference, product, or quotient. - Find .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Match the equation with the correct graph. -
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Consider the function h as defined. Find functions f and g so that (f ∘ g) (x) = h(x) . -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the function.
-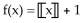
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the function.
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Consider the function h as defined. Find functions f and g so that (f ∘ g) (x) = h(x) . -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use a graphing calculator to solve the linear equation. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the slope of the line and sketch the graph.
-

A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Give the domain and range of the relation. -
A) domain: ; range:
B) domain: ; range:
C) domain: ; range:
D) domain: ; range:
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -In Country X, the average hourly wage in dollars from 1960 to 2010 can be modeled by Use to estimate the average hourly wages in 1965,1985 , and
A)
B)
C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the line described.
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The graph of a linear function f is shown. Write the equation that defines f. Write the equation in slope -intercept form.
-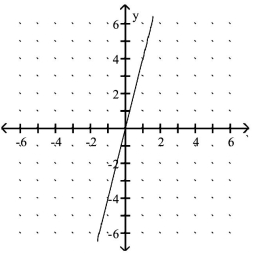
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Give the domain and range of the relation.
-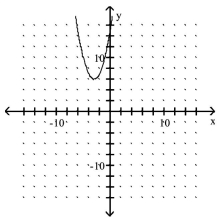
A) domain: ; range:
B) domain: ; range:
C) domain: ; range:
D) domain: ; range:
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the point symmetric to the given point.
-Plot the point (-2, -1) , then plot the point that is symmetric to (-2, -1) with respect to the x-axis. 
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Decide whether the relation defines a function. -
A) Function
B) Not a function
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the equation has a graph that is symmetric with respect to the y -axis, the x-axis, the origin, or none of these. -y = (x - 6) (x + 3)
A) y-axis only
B) none of these
C) x-axis only
D) x-axis, y-axis, origin
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the equation by plotting points.
-
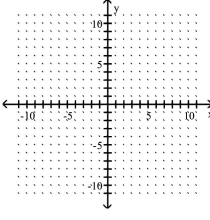
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write an equation for the line described. Give your answer in standard form. -through , undefined slope
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Describe the transformations and give the equation for the graph.
-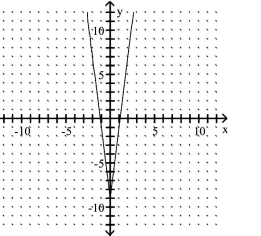
A) It is the graph of shrunken vertically by a factor of 8 and translated 9 units down. The equation is
B) It is the graph of stretched vertically by a factor of 8 and translated 9 units down. The equation is
C) It is the graph of stretched vertically by a factor of 8 and translated 9 units down. The equation is
D) It is the graph of shrunken vertically by a factor of 8 and translated 9 units down. The equation is
Correct Answer

verified
Correct Answer
verified
Showing 101 - 120 of 525
Related Exams