Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the gradient vector field  f(x,y) of f(x, y) =
f(x,y) of f(x, y) = 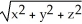 .
.
A) - ![]() i -
i - ![]() j -
j - ![]() k
k
B) ![]() i +
i + ![]() j +
j + ![]() k
k
C) ![]() i +
i + ![]() j +
j + ![]() k
k
D) ![]() i +
i + ![]() j +
j + ![]() k
k
E) - ![]() i -
i - ![]() j -
j - ![]() k
k
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the fact that the field F = 2x 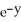 sin(z) i -
sin(z) i - 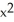
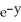 sin(z) j + (
sin(z) j + ( 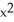
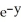 cos(z) + y) k is almost conservative (except for the last term) to help you evaluate
cos(z) + y) k is almost conservative (except for the last term) to help you evaluate 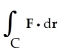 around the circle
around the circle 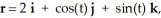

A) 2
B)
C) ![]()
D) ![]()
E) 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find parametric equations of the streamline of the velocity field v(x, y, z) = y i - y j + y k that passes through the point (2, -3, -4) .
A) x = 2 + t, y = -3 - t, z = -4 + t
B) x = 2 + t, y = -3 + t, z = -4 + t
C) x = 2 + t, y = -3 - t, z = -4 - t
D) x = 2 + t, y = 3 - t, z = 4 + t
E) x = 2t, y = -3t, z = -4t
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate the line integral 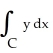 + x dy + z dz along the curve C from (1, 0, 1) to(-1, 2, 5) with parametrization
+ x dy + z dz along the curve C from (1, 0, 1) to(-1, 2, 5) with parametrization 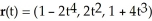 with
with 
A) 9
B) 10
C) 11
D) 12
E) 8
Correct Answer

verified
Correct Answer
verified
Short Answer
Let F be a smooth conservative force field defined in 2-space with a potential function 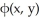 , and let C be the curve shown in the figure below. Find the work done by the force field F in moving a particle along the curve C from P to R given that φ(1,- 2) = -17, andφ(4, 1) = 3.
, and let C be the curve shown in the figure below. Find the work done by the force field F in moving a particle along the curve C from P to R given that φ(1,- 2) = -17, andφ(4, 1) = 3. 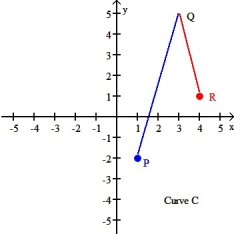
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The gradient of a scalar field ![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee7ba9_d077_68d8_ae82_6357d8c80115_TB9661_11.jpg) expressed in terms of polar coordinates [r, ] in the plane is
expressed in terms of polar coordinates [r, ] in the plane is![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee7ba1_8550_5724_ae82_1fed9cde7479_TB9661_11.jpg) (r, ) =
(r, ) = ![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_779c_de41_a0f8_0f3ea7ccd08b_TB9661_11.jpg)
![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_779c_de42_a0f8_2fd44569cc80_TB9661_11.jpg) +
+ ![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_779c_de43_a0f8_61d586b44d12_TB9661_11.jpg) .
. ![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_779c_de44_a0f8_b346e40bf9b3_TB9661_11.jpg)
![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_779c_de45_a0f8_93245f5dc084_TB9661_11.jpg) Use the result above to find the necessary condition for the vector field F(r, ) = P(r, )
Use the result above to find the necessary condition for the vector field F(r, ) = P(r, ) ![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_779c_de46_a0f8_0766653367fc_TB9661_11.jpg) + Q(r, )
+ Q(r, ) ![The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative. A) = B) = r C) = - D) - r = Q E) - = r](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_779c_de47_a0f8_01b43d2ef1f7_TB9661_11.jpg) to be conservative.
to be conservative.
A) ![]() =
= ![]()
B) ![]() = r
= r ![]()
C) ![]() = -
= - ![]()
![]()
D) ![]() - r
- r ![]() = Q
= Q
E) ![]() -
- ![]() = r
= r
Correct Answer

verified
Correct Answer
verified
Short Answer
Find the area element at a point r (θ, φ) on the parametric surface  ,
, 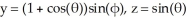 .
.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
(a) In terms of polar coordinates r and , describe the field lines of the conservative plane vector field F(x,y) = x i + y j. (b) In terms of polar coordinates r and , describe the equipotential curves of the conservative plane vector field F(x,y) = x i + y j.
A) (a) radial lines = ![]() (b) circles r =
(b) circles r = ![]()
B) (a) circles r = ![]() (b) radial lines =
(b) radial lines = ![]()
C) (a) circles r = ![]() sin( ) (b) circles r =
sin( ) (b) circles r = ![]() cos( )
cos( )
D) (a) lines r cos = ![]() (b) lines r sin =
(b) lines r sin = ![]()
E) (a) lines r cos = ![]() (b) radial lines =
(b) radial lines = ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area of the region cut from the plane x + 2y + 2z = 5 by the cylinder whose walls are 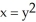 and
and 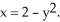
A) 2 square units
B) 3 square units
C) 4 square units
D) 6 square units
E) 1 square unit
Correct Answer

verified
Correct Answer
verified
Multiple Choice
How much work is required for the force field F = y i + 2x j to move an object along the upper part of the ellipse 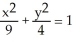 from (3, 0) to (-3, 0) ?
from (3, 0) to (-3, 0) ?
A) 2
B) 9
C) -9
D) -2
E) 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Compute the flux of F = z  i -
i -  y j + (x - 2z) k upward across the square
y j + (x - 2z) k upward across the square 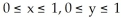 in the plane z = 1.
in the plane z = 1.
A) ![]()
B) - ![]()
C) - ![]()
D) ![]()
E) 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the value of the positive constant real number a such that the area of the part of the plane 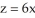 inside the elliptic paraboloid z = 3x2 + ay2 is equal to
inside the elliptic paraboloid z = 3x2 + ay2 is equal to 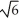 square units.
square units.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
If F = -y i + x j + z k, calculate  where C is the straight line segment from(1, 0, 0) to (-1, 0, ) .
where C is the straight line segment from(1, 0, 0) to (-1, 0, ) .
A) ![]()
B) ![]()
C) 1
D) ![]()
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Is F (x,y) = (3  y + 2x
y + 2x 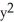 + 1) i + (
+ 1) i + ( 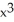 + 2
+ 2 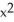 y + 1) j conservative? If so, find a potential for it.
y + 1) j conservative? If so, find a potential for it.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) No, it is not conservative.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate 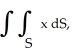 where S is the part of the paraboloid 2x = 8 -
where S is the part of the paraboloid 2x = 8 - 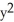 -
- 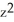 lying between the planes
lying between the planes 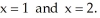
A) 2 ![]()
B) 2 ![]()
C) 2 ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Let 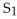 =
= 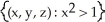 ,
,  =
= 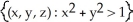 and
and  =
= 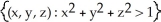 be sets of points in 3-space. Determine whether the set is a connected or a simply connected set.
be sets of points in 3-space. Determine whether the set is a connected or a simply connected set.
A) S1 is simply connected.
B) S2 is not connected.
C) S1 is connected but not simply connected.
D) S3 is simply connected.
E) S3 is connected but not simply connected.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Compute the flux of F = 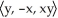 outward from the solid region
outward from the solid region 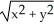 z 1.
z 1.
A) -2
B) 2
C) 1
D) 0
E) -1
Correct Answer

verified
Correct Answer
verified
True/False
The function V(x,y) = 3 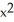 +3xy + 5
+3xy + 5  is a Liapunov function for the autonomous system associated with the vector field F = (y -7x) i + (3x - 5y) j in any domain D containing the fixed point at the origin.
is a Liapunov function for the autonomous system associated with the vector field F = (y -7x) i + (3x - 5y) j in any domain D containing the fixed point at the origin.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Compute the flux of F = 2x i - 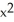 j + (z - 2x + 2y) k upward through the part of the plane
j + (z - 2x + 2y) k upward through the part of the plane 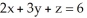 in the first octant of 3-space.
in the first octant of 3-space.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) 0
Correct Answer

verified
Correct Answer
verified
Showing 21 - 40 of 90
Related Exams