A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find all the roots of the function. Use preliminary analysis and graphing to determine good initial approximations. Round to six decimal places.
-f(x) = cos 4x - 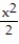 + 5
+ 5
A) x -4.859572, 1.859572
B) x -3.470572, 3.248572
C) x -3.248572, 3.470572
D) x -3.359572, 3.359572
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Sketch the graph and show all local extrema and inflection points.
-y = - 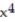 + 4
+ 4 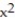 - 2
- 2
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use l'Hopital's Rule to evaluate the limit.
-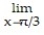
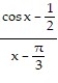
A) ![]()
B) - ![]()
C) ![]()
D) - ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the linearization L(x) of f(x) at x = a.
-f(x) =  , a = 0
, a = 0
A) L(x) = 1/4 x
B) L(x) = -1/4 x
C) L(x) = - 1/2 x
D) L(x) = 1/2 x
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the extreme values of the function and where they occur.
-y = 
A) Absolute maximum value is 0 at x = 0.
B) Absolute minimum value is 0 at x = 1. Absolute maximum value is 0 at x = -1.
C) Absolute minimum value is - 1 at x = -1. Absolute maximum value is 1at x = 1.
D) Absolute minimum value is 0 at x = 0.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the indefinite integral. Check your work by differentiation.
-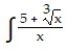 dx
dx
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find an antiderivative of the given function.
-2 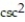

A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Sketch the graph and show all local extrema and inflection points.
-y = x 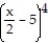
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
True/False
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-g(x) = 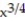 ,
, 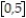
Correct Answer

verified
Correct Answer
verified
Multiple Choice
L'Hopital's rule does not help with the given limit. Find the limit some other way.
-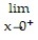
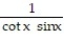
A) -1
B) 0
C)
D) 1
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Express the relationship between a small change in x and the corresponding change in y in the form 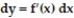 .
-y = x
.
-y = x 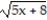
A) ![]()
B) ![]()
C)
![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find an antiderivative of the given function.
-- 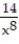
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.
-At about what velocity do you enter the water is you jump from a 15 meter cliff? (Use g = 9.8 m/ 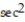 .)
.)
A) 2 m/sec
B) -8.5 m/sec
C) -17 m/sec
D) 17 m/sec
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the largest open interval where the function is changing as requested.
-Decreasing f(x) = 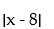
A) (- , -8)
B) (8, )
C) (- , 8)
D) (-8, )
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.
-A company is constructing an open-top, square-based, rectangular metal tank that will have a volume of  What dimensions yield the minimum surface area? Round to the nearest tenth, if necessary.
What dimensions yield the minimum surface area? Round to the nearest tenth, if necessary.
A) 5.1 ft × 5.1 ft × 1.7 ft
B) 3.5 ft × 3.5 ft × 3.5 ft
C) 4.5 ft × 4.5 ft × 2.2 ft
D) 9.4 ft × 9.4 ft × 0.5 ft
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the most general antiderivative.
- d
d
A) cot + C
B) + tan + C
C) -cot + C
D) ![]() + C
+ C
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the absolute extreme values of the function on the interval.
-F(x) = 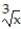 , -1 x 27
, -1 x 27
A) absolute maximum is 3 at x = 27; absolute minimum is 0 at x =0
B) absolute maximum is 3 at x = 27; absolute minimum is -3 at x = -27
C) absolute maximum is 0 at x = 0; absolute minimum is 3 at x = 27
D) absolute maximum is 3 at x = -27; absolute minimum is 0 at x =0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the absolute extreme values of the function on the interval.
-h(x) = 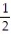 x + 5, -2 x 3
x + 5, -2 x 3
A) absolute maximum is - 7/2 at x = -2; absolute minimum is 4 at x = 3
B) absolute maximum is 13/2 at x = 3; absolute minimum is 4 at x = -2
C) absolute maximum is - 7/2 at x = -3; absolute minimum is -3 at x = 2
D) absolute maximum is - 7/2 at x = 3; absolute minimum is 4 at x = -2
Correct Answer

verified
Correct Answer
verified
True/False
Use differentiation to determine whether the integral formula is correct.
-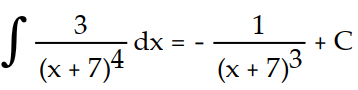
Correct Answer

verified
Correct Answer
verified
Showing 181 - 200 of 228
Related Exams